[10000印刷√] 三角形辺の長さ求め方 314217-三角形辺の長さ求め方

 直角三角形の3辺の長さの関係を表したもの だよ その関係っていうのは、 斜辺2 = 底辺2 高さ2 斜 辺 2 = 底 辺 2 高 さ 2 だよB, c , a が与えられているとき、直角三角形 ahc の3辺の長さが求まるので、 hb , hc の値から三平方の定理を使って bc を求めます。 右図6において、頂点 C から辺 AB に引いた垂線を CH とする。 次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。

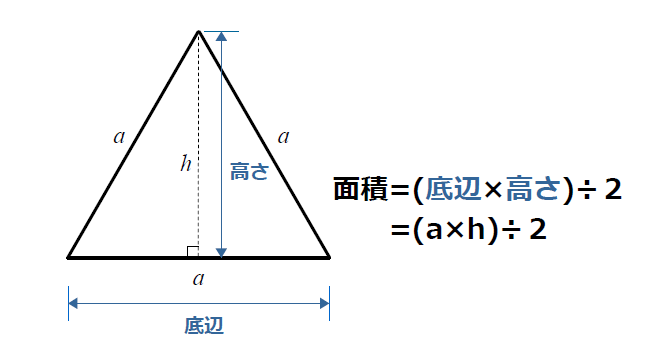
二等辺三角形の面積を求める算数の公式は

三角形辺の長さ求め方

三角形辺の長さ求め方-このように，相似な三角形は対応する辺の比が等しいので，辺の比さえ分かってしまえば， どのように大きな三角形の辺の長さも，すぐに求めることができる。 直角三角形の場合，直角以外の1 つの角が決まると相似となるので，三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺) ・ 直角三角形 (底辺と角度) ・ 直角三角形 (高さと斜辺) ・ 直角三角形 (高さと角度)

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

S = 1 2 r ( a b c) 「3辺の長さ a, b, c 、外接円の半径 R の三角形」の面積は S = a b c 4 R で求められます。 ただ、これらの公式を使わなくても3辺の長さ a, b, c の値が分かっている時点で「④ ヘロンの公式」を使えば三角形の面積を求めることは可能です三角形abc で，頂点a, b, c に対する辺の長さ を，それぞれ，a, b, c とする。また∠a, ∠b, ∠c の 大きさを，それぞれa, b, c と書くことにする。 このとき次の定理が成立する。 ここでr は三角形abc の外接円の半径である。 証明 外接円の中心をo とする。直角三角形の解法とは たとえば、次のような直角三角形を考えてみましょう。 直角三角形ですから、c = 90度であることはあらかじめわかります。それでは、次のように、一部の角の大きさや辺の長さが分かっていて、残りが分からないという場合を考えて

Ama02 練習問題へ u adc は直角三角形であるから，ac の長さがわかればad の長さが求められる。 そこで，ま ず，u abc に注目し，三平方の定理を利用して，ac の長さを求める。 u abc で三平方の定理より ac 5 5 10 5 cm＝－＝（）_i2 2 ←ac ab bc＝－22 さらに，u adc で三平方の定理より理由は「正三角形の頂角の二等分線は底辺の垂直二等分線と一致する」からです。 関連： 二等辺三角形の4つの性質と4つの条件 A B = x として、 B M 、 A M の長さを計算してみましょう。 M は B C の中点なので B M = 1 2 B C = 1 2 x となります。 斜辺をb、等しい辺の長さをaとすると、 a = √2b /2

S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B たとえば3つの角がすべて60°とわかれば正三角形まではわかります（辺の比1：1：1）。しかし，その長さは求めることができません。辺の比を求める方法は正弦定理を使えばOKです。 正弦定理より\(\displaystyle \frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}} \)なので 三平方の定理を使って直角三角形の辺の長さを計算したい！ どうも、Drリードだぞい。 中3数学では、 三平方の定理（ピタゴラスの定理） を勉強してきたよな？ 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²＋ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

正弦定理から，三角形の辺の長さを求める計算について ABCにおいて a = 3 ， A = 60°， B = 45°のとき b を求めよ。 という問題がありますが， これを定理にあてはめていって， b = 3 / sin60°× sin45° まではつくれるんですが，そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが，意味がわかりません。 なぜルートが出てくるのですか？ (3 ÷√3/2)×1/√2が，もう何 直角三角形ahcにおいて、三平方の定理を使うだけです。 ac=√(ah^2ch^2) =√(4864) =4√7 となり、対角線の長さacが求められました。 多角形の対角線の本数の求め方 多角形の対角線の本数は、いちいち引いて数えなくても公式を使って一瞬で求められます。直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度

Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ

高校数学 三角比 辺の長さの求め方まとめと問題

 正三角形の性質と辺の長さを求める頻出の問題をみてみましょう。 性質 正三角形とは、三辺の長さが全て等しい三角形のことを言います。 様々な三角形がある中で、辺の長さが全て等しいという特殊性を備え、それ故にいくつかの性質が導かれます。二等辺三角形の角度は、頂角が分かれば低角を求めることが可能です。 二等辺三角形の2つの低角は同じ値になるからです。 例えば、頂角が90度のとき2つの低角は45度です。 今回は二等辺三角形の角度、求め方、辺の長さとの関係について説明します 定義や辺の長さの比、面積の求め方 受験辞典 直角二等辺三角形とは？ 定義や辺の長さの比、面積の求め方 この記事では、「直角二等辺三角形」の定義や公式、辺の長さの比などについて解説していきます。 また証明問題もわかりやすく説明していく

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

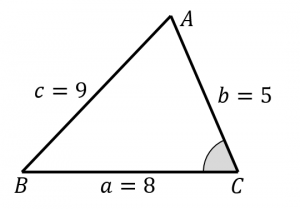
三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

 21年2月19日 この記事では、「三角形」の面積公式や角度・辺の長さ・重心の求め方などを紹介していきます。 また合同条件や、比の計算問題の解き方も詳しく解説していくので、ぜひマスターしてくださいね！ 目次 非表示 三角形とは？ 三角形の面積の公式 公式①底辺 × 高さ ÷ 2 公式②三角比の面積公式 公式③ヘロンの公式2辺a,bと高さ（角Cは鋭角）選択で 辺a=5 辺b=6 高さ=3で計算したとき、角Aの値がマイナスになります。 keisanより ご指摘ありがとうございます。修正いたしました。三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 （右図イのような場合も含めて）一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。

高校数 三角比 三角形の面積 ３辺の長さから オンライン無料塾 ターンナップ Youtube

三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

三角形の辺の長さを求めるときの三角比の値 下の図の x の値を求めよ。 これを解こうとすると，sin45°，sin60°という三角比が出てきました。直角三角形の辺を求める 直角三角形の辺を求める Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your三角形の3辺が与えられたときの面積の求め方 「3辺の長さが，5，4，7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは，公式 S＝1/2bc sinA に当てはめればいいことは

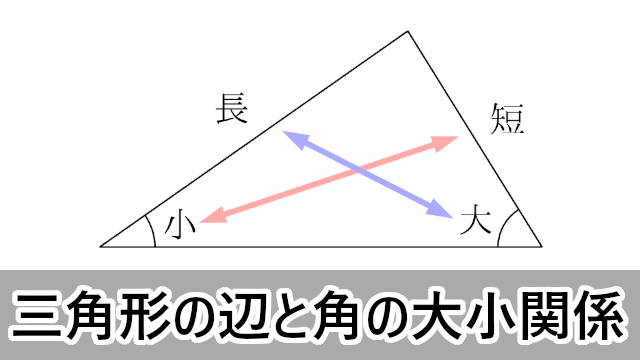
数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法

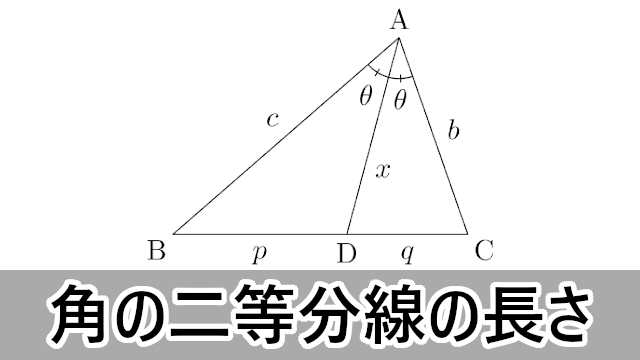
数学ia 三角形の内角の二等分線の長さ 大学入試数学の考え方と解法

 二等辺三角形の底辺の長さの求め方がわかる3ステップ さっきの例題をといてみよう。 つぎの二等辺三角形ABCの底辺BCの長さを求めなさい。 なお、AB = BC = 6 cm、角B = 角C = 30°とします。 つぎの3ステップで計算できちゃうよ。 Step1 頂角の二等分線を底辺S formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問具体例で学ぶ数学 > 図形 > 直角二等辺三角形の辺の長さの求め方 最終更新日 直角二等辺三角形において、 (斜辺の長さ) = 2 × (他の辺の長さ) （ 2 はだいたい 14 ） 目次

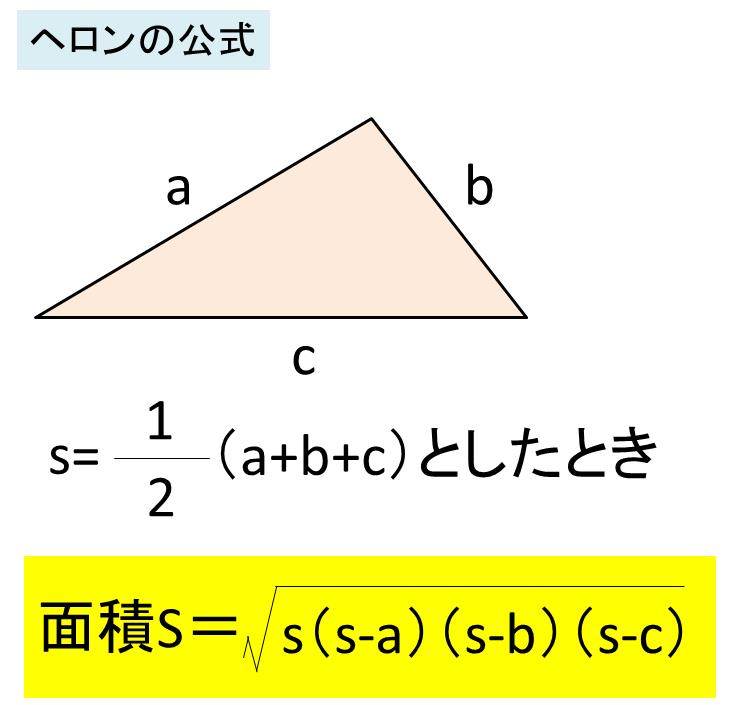
Excel エクセルでヘロンの公式により三角形の面積を求める方法 計算

数学の勉強 三角比

直角二等辺三角形の辺の長さは？1分でわかる求め方、公式、辺の長さと角度の関係、証明 二等辺三角形の底辺と高さの関係 二等辺三角形の底角をθ、斜辺をa、高さをh、底辺の長さをLとするとき、下記の関係になります。 sinθ＝h/a cosθ＝L/a正弦定理は三角形の問題を解くのに便利な方法です。 特に、直角三角形の一辺の長さと直角以外のいずれかの角の角度が分かれば、斜辺の長さが求められます。 辺 a 、 b 、 c と、角 A 、 B 、 C の三角形があるとすると、正弦定理は a / sin A = b / sin B = c / sin以上から直角三角形 $\text{ABC}$ の3辺の長さは、図のようになる。 $15^\circ$、$75^\circ$、$90^\circ$ の三角形 これより、$15^\circ$ の三角比は以下のように求められる。

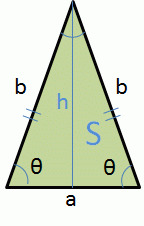
三角形の公式 Wakatta

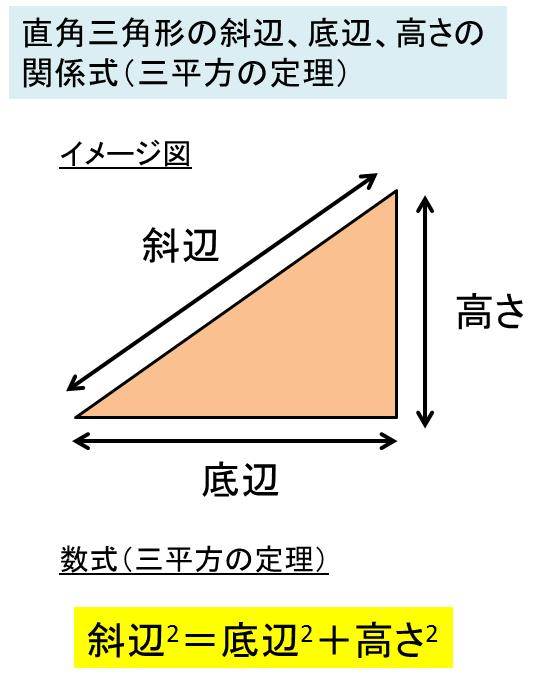
Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

直角三角形の直角をはさむ2つの辺の長さを a 、 b として、長い辺の長さを c とします。 このとき、 a × a b × b = c × c が成立します。 これを三平方の定理、またはピタゴラスの定理と言います。 例題1： 図のような直角三角形の長い辺の長さを求めよ。 長い辺の長さを c とすると、 2 × 2About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

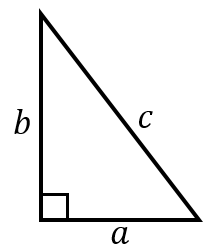
直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学

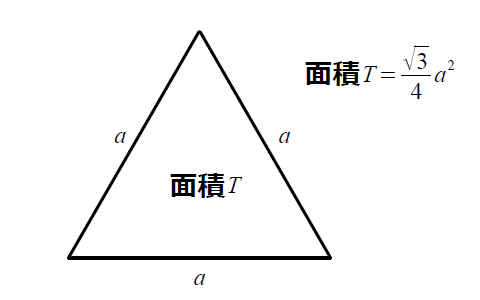
正三角形の面積計算 ゆるゆるプログラミング

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

二等辺三角形の面積を求める算数の公式は

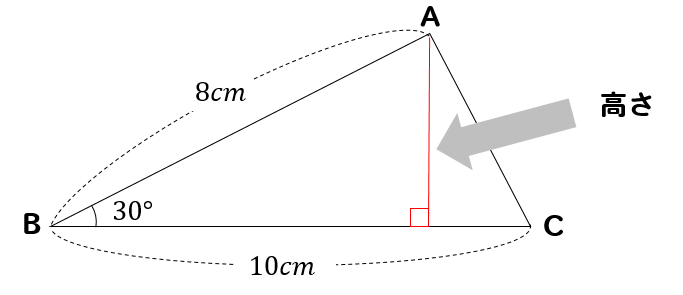
小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ

直角三角形の辺の長さ 合同条件 面積について アタリマエ

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

高校数学 ３辺 三角形の面積 を求める方法 映像授業のtry It トライイット

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

三平方の定理 自動計算サイト

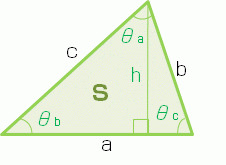
三角形の公式 Wakatta

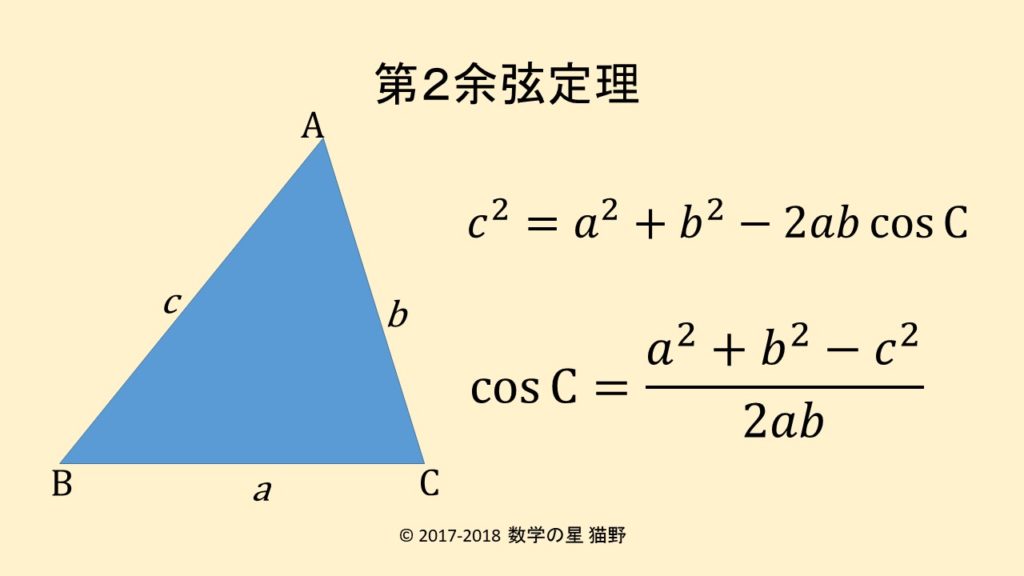
第２余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

余弦定理で角度を求める方法 数学の星

高校数学でよく使う三角形の面積公式まとめ おいしい数学

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

直角三角形の斜辺の長さを求める 3つの方法 Wikihow

直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学

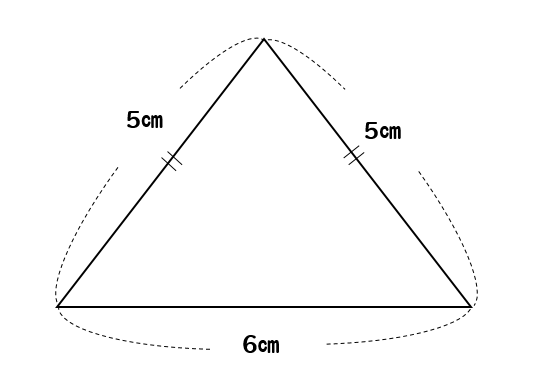
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

48s96ub7b0z5f Net Bekutoru Menseki

平面図形の苦手を解消 三角形の面積比 基本編

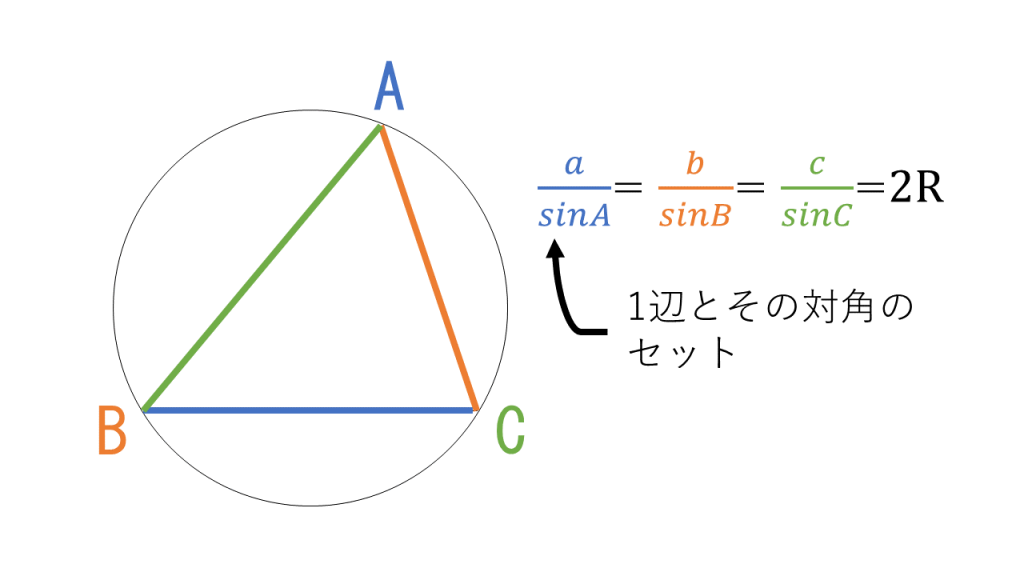
3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ

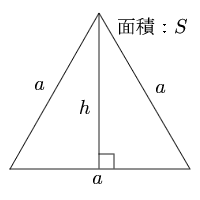
正三角形 面積から辺と高さ 三角形の計算 計算サイト

面積の求め方 計算公式一覧

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

直角三角形の解法 1

中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

高校入試 英語 数学 特別な直角三角形

3

直角三角形 Wikipedia

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

面積分割

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

3

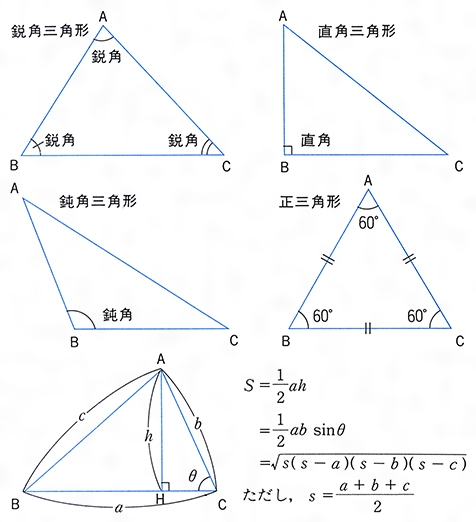
三角形とは コトバンク

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

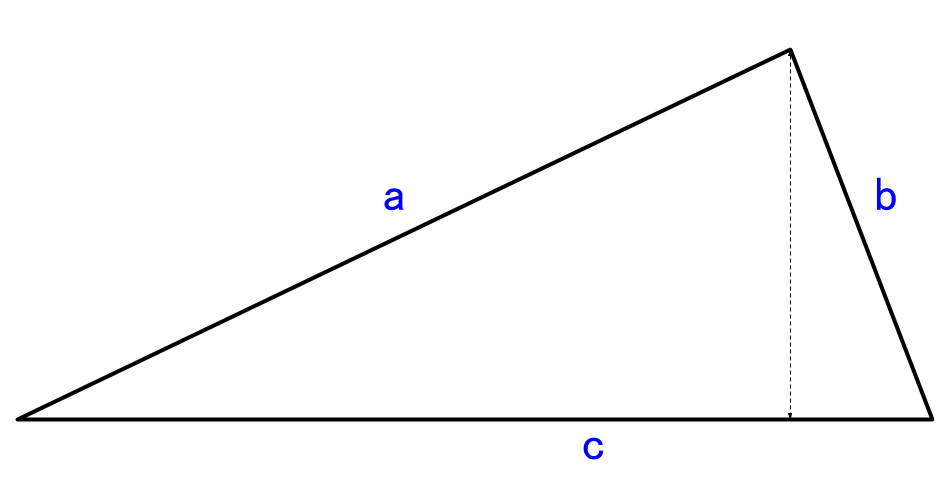
ヘロンの公式 計算機 三角形の面積と高さを 3辺の長さから計算します やまでら くみこ のレシピ

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

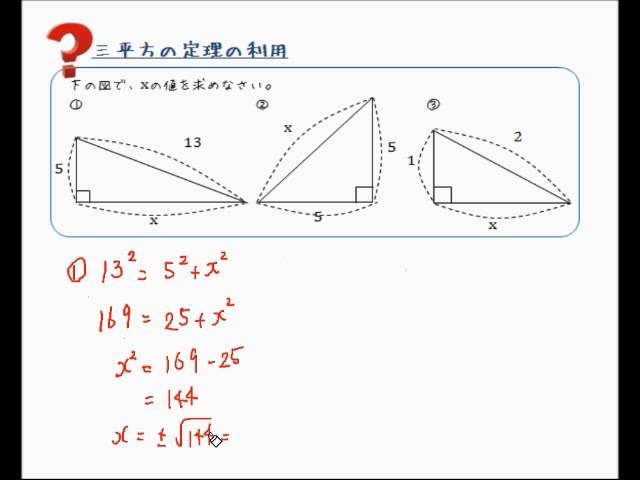
三平方の定理で辺を求める Youtube

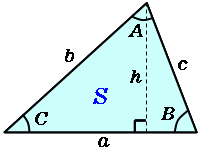
不等辺三角形 高精度計算サイト

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

1

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

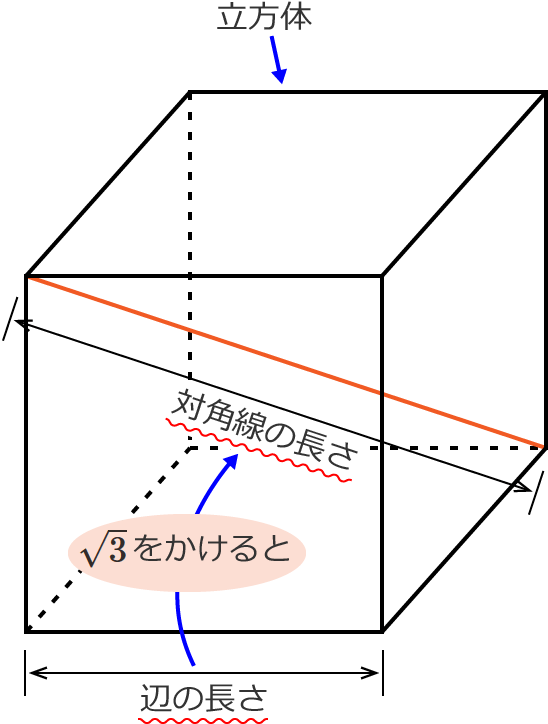
立方体の対角線の長さの求め方

数i 基本的な三角比の値

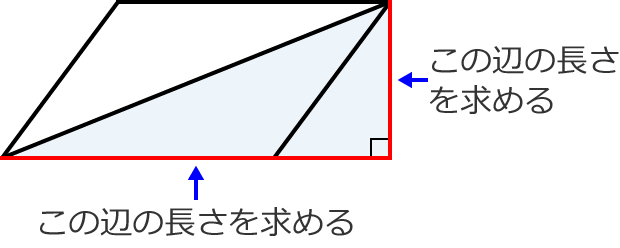
平行四辺形の対角線の長さの求め方

三角比から辺の長さを求める 数学i フリー教材開発コミュニティ Ftext

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

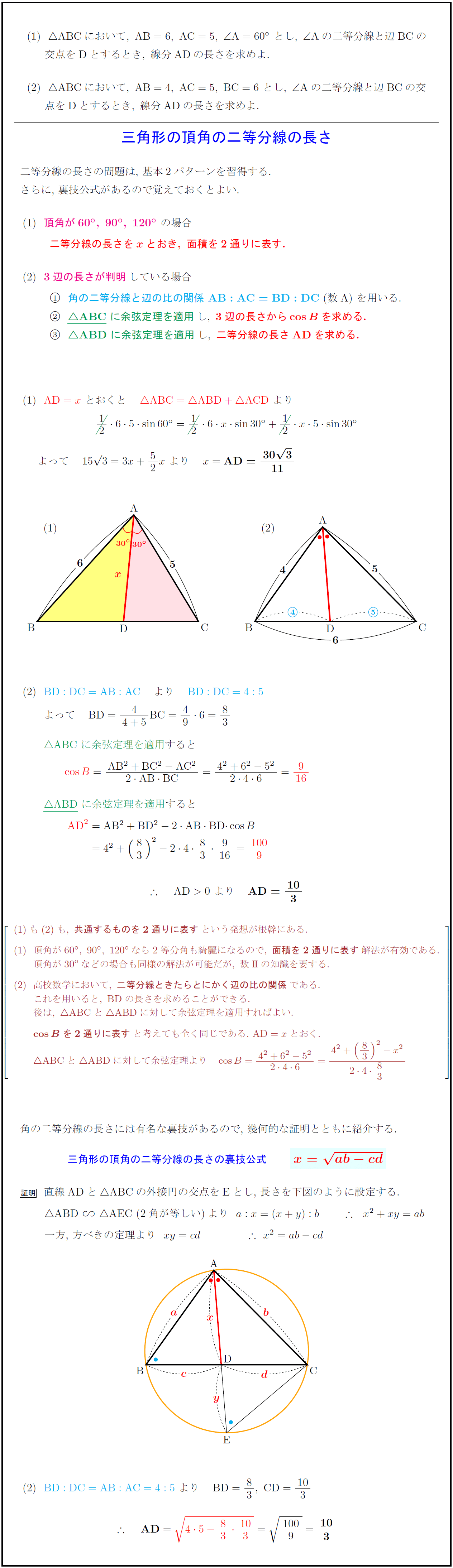
高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

直角三角形の辺を求める Youtube

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

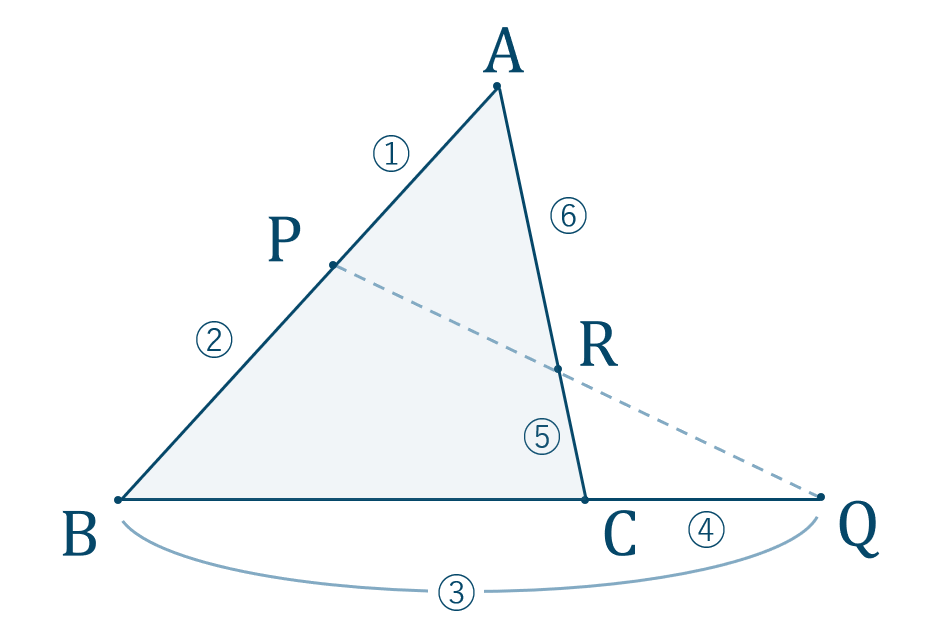
公式一覧と使い方 解き方 数学ａ 図形の性質 教科書より詳しい高校数学

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円の中の三角形の一辺の求め方がわかりません お恥ずかしい話ですが 仕事で Yahoo 知恵袋

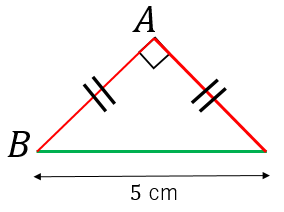
直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

面積の求め方 計算公式一覧

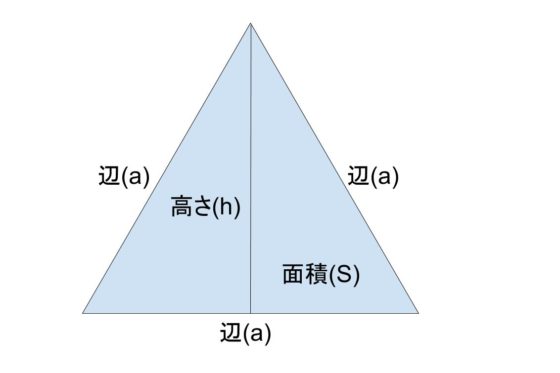
正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

直角三角形の解法 1

三平方の定理の証明と使い方

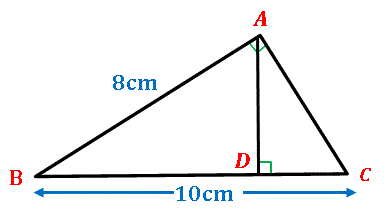
直角三角形の辺の長さを求めましょう

直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明

底辺と高さから角度と斜辺を計算 高精度計算サイト

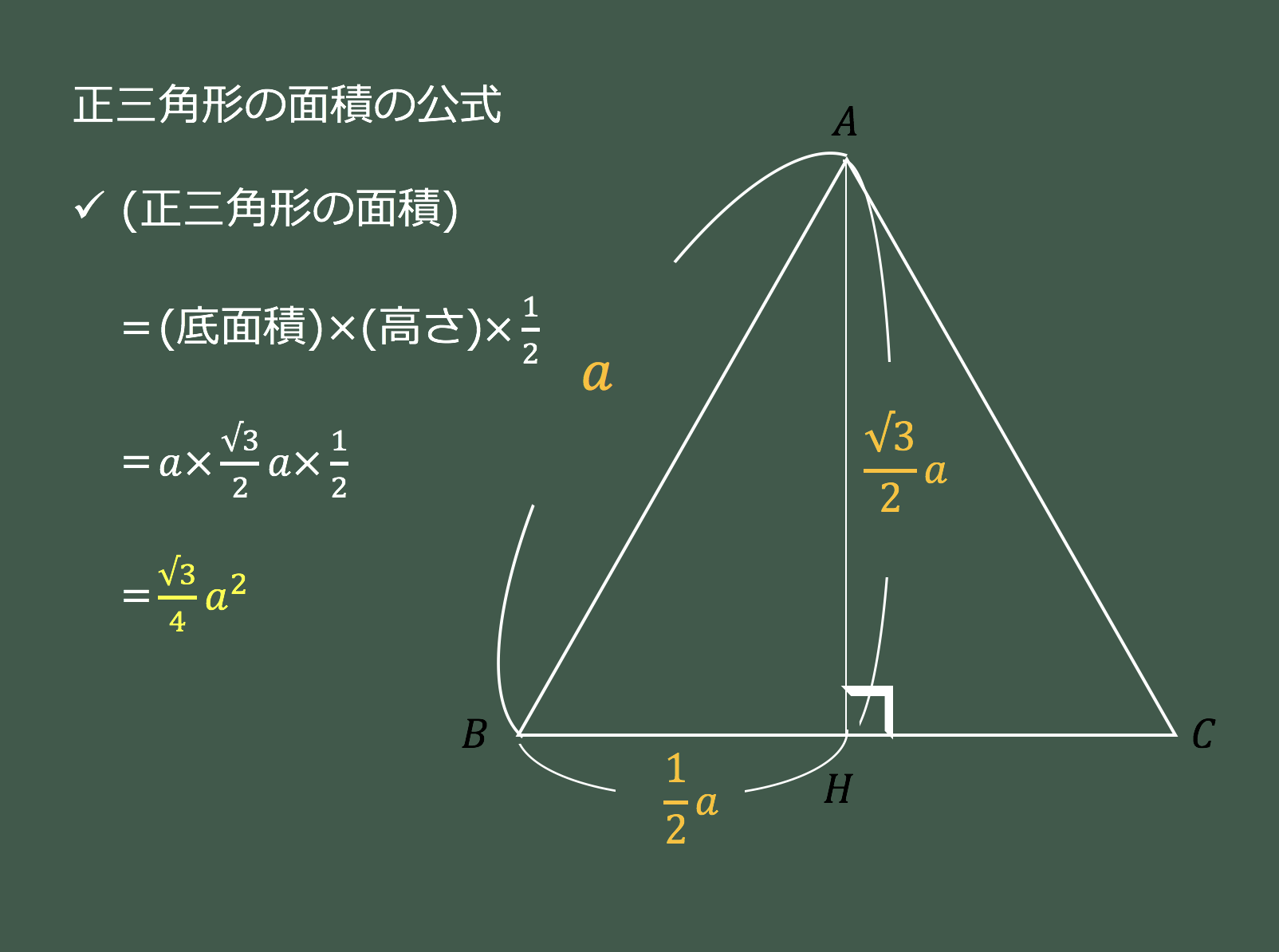
3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

高校数学 三角形の辺と角の関係 映像授業のtry It トライイット

三角関数 1 Cg 数学 06aa

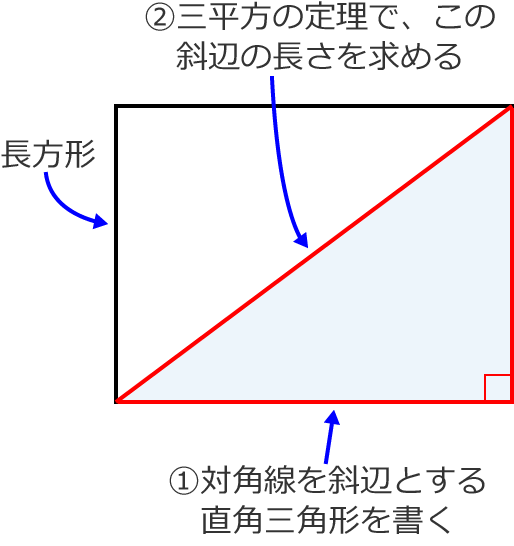
長方形の対角線の長さの求め方

正三角形の面積計算 ゆるゆるプログラミング

Incoming Term: 三角形辺の長さ求め方, 三角形辺の長さ求め方 小学生,