等比数列 一般項 求め方 478992-等比数列 一般項 求め方

19/5/21 等比数列の一般項の求め方 それでは、数列を考えるのに重要な「一般項」の求め方を考えていきましょう。 まず、等比数列は次のような数列となってました。 ※ 初項が「1」、公比が「2」の例としております。 この数列の一般項の求め方 2233 2^2，4^2，6^2，8^2，・・・・ 簡単な数列なのですが、一般項の求め方で悩んでいます。 しらみつぶしではない解法です。 答えはan＝（2n）^2です。 等比数列だからar^n1＝anに当てはめるのでしょうか？また、フィボナッチ数列の一般項の求め方には様々な方法がありますが、ここでは一番オーソドックスな解き方を説明することとします。 フィボナッチ数列とは$ a_ {n2}=a_ {n1}a_n$という漸化式と、 第一項と第二項がそれぞれ$ a_1=1$、$ a_2=1 $によって与え 数

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列 一般項 求め方

等比数列 一般項 求め方-28/2/ F n = F n − 1 F n − 2 ( n ≧ 2) フィボナッチ数列は0, 1から始まり、その後の項は直前の2つの項の和となっている数列です。 1000万以下のフィボナッチ数列の項は以下のようになります。 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, , , , , , , , , , 40, , , ,のような形になっているとき，このままの形では数列 は，等比数列にはなりませんが， (2') と変形すると，数列 は等比数列になるので のように一般項が求められます． ≪変形のポイント≫ (2)式を (2')式に変形するためのポイントは となる定数 を係数比較によって求めることです． を (2)式と係数比較すると となって

例題で学ぶ高校数学 等差数列 等比数列 型の数列

この映像授業では「高校 数学B 数列9 等比数列の一般項2」が約18分で学べます。問題を解くポイントは「等比数列の一般項は、an＝初項×公比等比数列（とうさすうれつ）の一般項は「ar (n－1) 」で算定します。 aは初項、rは公比、nは第n項のことです。 等比数列とは「1、2、4、8」のような数列です。2/3/09 等比数列：an=a1r^ (n1) ただし、a1：初項 r：公比 a4=a1r^3=2 a7=a1r^6=16 から比較すると r^3=8 あとはできるでしょ。

24/6/12 等比数列 求め方｡ ・公比2､第5項が80 この時の一般項。 ・第2項－6､第5項162 この時の一般項。 ・数列8,a,2/9,b が等比数列であるとき､a,bの値｡29/7/19 > 求めたい等比数列の一般項は > a_n=2*n1 これはなんか数学的に用語が間違ってる気がしますね。そのa_nであれば等差数列だし、求めたいものは階差が等差数列になる数列で等比数列でもないです。 それはともかく「再帰」などで検索してみては。27/6/19 3．一般項： { a_n=a \cdot r^ {n1} \ \ (n=1,2,3, \cdots) \ (a,r定数) } 定 数 定数 r は，等比数列の公比（こうひ）という． 狭義の等比数列では， r≠0, 1 として扱うが，本記事では，先ずは, スタンダードに, r≠0, 1 の場合について議論して, 一般項を求める。その後

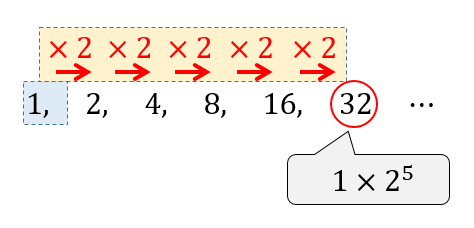
24/5/18 等差数列の一般項 数列で大事なことは一般項を求めることでした。 要するに 第何項目がどんな数字なのかがすぐわかるような式を用意したい ということです。 一般項は慣習上 \ (a_ {n}\) で表します。 これは第 \ (n\) 項目がなんなのかを表す意味が込め階差型の数列 タイプ： 教科書範囲 レベル： ★★ 階差数列を用いて一般項を求める方法について解説します． 当サイトではそのような数列を階差型の数列と呼ぶことにし，深く内容を考察，解説し，演習問題まで用意しました． 目次 1： 階差型の数列12/3/ 等比数列の一般項と和の求め方 では次に、等比数列の一般項とその和の求め方について説明します。 等比数列とは、たとえば次のように項が増えるごとにある数が掛け合わされていく数列のことです。 $$2, \quad 6,\quad 18,\quad 54,\quad 162,\quad 486,\quad 1458, \quad \cdots$$

等比数列の和の公式の証明といろいろな例 高校数学の美しい物語

特殊な和の求め方その２ 等差 等比編 高校数学の知識庫

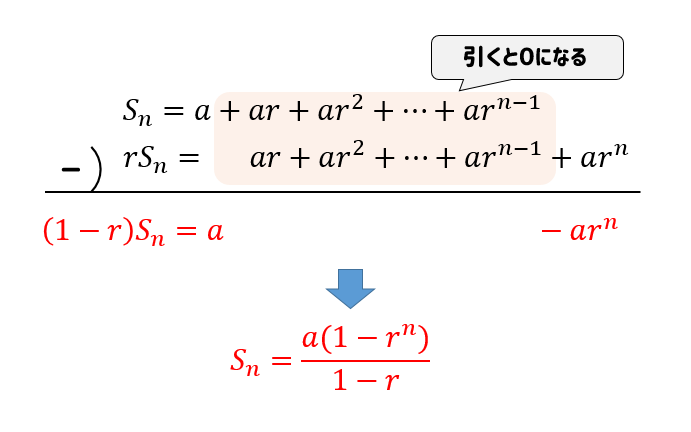
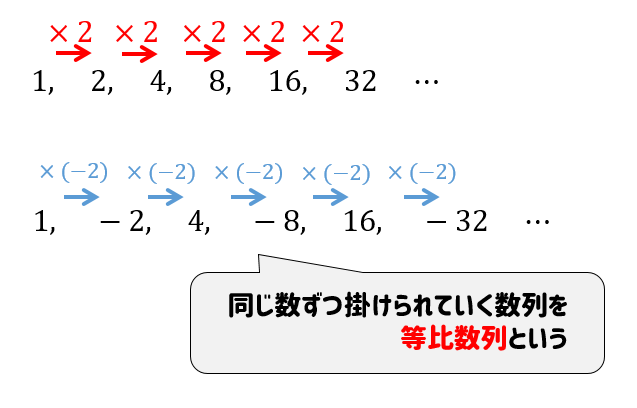
等比数列の一般項を求める公式 $$a_n=ar^{n1}$$ $$a初項 r公比$$ 等比中項 3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。 $$b^2=ac$$ 等比数列の和を求める公式 \(r\neq 1\) のとき $$S_n=\frac{a(1r^n)}{1r}=\frac{a(r^n1)}{r1}$$ \(r=1\) のとき $$S_n=na$$第２項は［2］の式を𝑎 n =𝑎 1 と考えて計算を行うことで求めることが出来る。 つまり𝑎 2 =3×22=8となる。 第３項は［2］の式を𝑎 n =𝑎 2 と考えて計算を行うことで求めることが出来る。 つまり𝑎 3 =3×=26となる。25/5/18 等比数列の一般項がわかったところで、等比数列のよく使う性質を紹介しておきます。 それは簡単に書くと次のようになります。 等比数列の連続する3つの数 a 、 b 、 c がこの順で並んでいるとき、これらには次の関係がある。 a × c = b 2 例えば先ほど

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

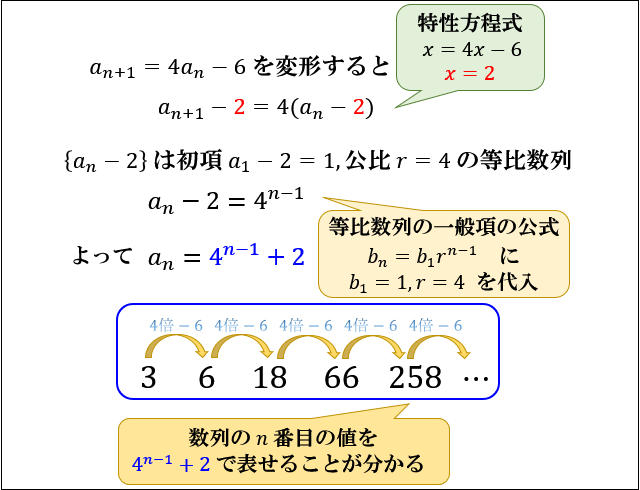
特性方程式とは より難しい漸化式の解き方 特殊解型 アタリマエ

11/6/18 {bn}の一般項は前回「等差・等比・階差数列型の一般項の求め方」と同じ方法等比数列型の漸化式を解くことで導出して、 \(b_{n}=12× 2^{n1}\) bn＝12×2^(n1)となります。 12＝2・2・3より \(b_{n}=3× 2^{n1}\)例題1 等比数列{a n}において，初項 3，a 4 =375 の公比 r と一般項 a n を求めよ。 解答 題意より一般項 a n は a n =3r n1 となる。a 4 =375 より，3r 41 =375 なので，r 3 =125=5 3 よって，r=5 ゆえに，一般項は a n =3･5 n1 次に，等比数列の典型的な問題を紹介します。の形であるならば，この数列 は，初項 公比 の等比数列だから，直ちに一般項が求まります．

Excel エクセルで等比数列の和を計算する方法

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の一般項を求める公式の証明と例題2問を解説します。第n項は初項×公比のn1乗です。 第n項は初項×公比のn1乗です。 算数から高度な数学まで、網羅的に解説した 等比数列一般項の求め方, 等比数列の一般項・和の公式とその応用（自然数×等比数列一般項はnの1次式で表される。したがって、原数列の一般項は、等差数列の和を考えると、nの2次式になるだろう。 ＜まなぶ＞ 余計、分からなくなりました。 ＜先 生＞ では階差数列が等比数列の場合を考えてみよう。初項b、公比rとすると、等差数列の和を求める公式 ：初項 ：末項 ；項数 等差数列の和を求めるときに使うのが上の公式です。 2パターンの公式があるのですが、別物だとは思わないでくださいね。 末項（ ）を一般項の公式を用いて、 として考えたのが下の式です。 こうやっ

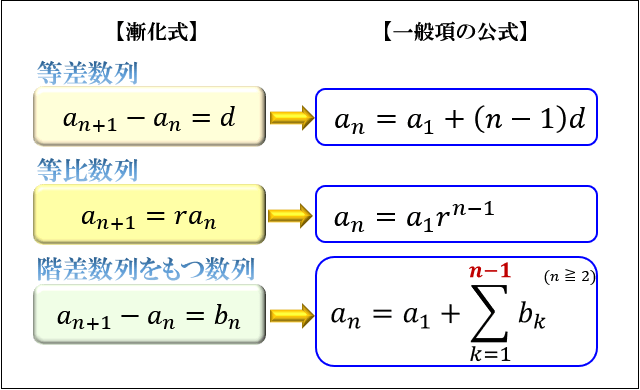
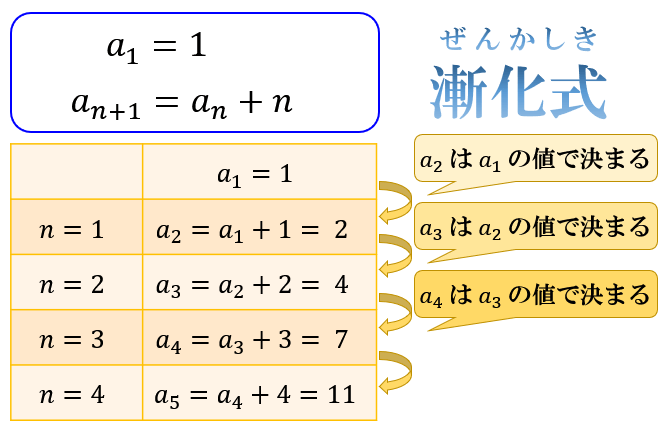
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等比 等差の和を求める２通りの方法 高校数学の美しい物語

一般項｛αⁿ｝は初項が2なので n≧2のとき n=1のとき 注意事項 上記の問題は のときに公式を使って求め のときに求めた式が成り立っているのかを確認することが解き方の基本となっている。等比数列の一般項の証明 等比数列は初項に対して公比を掛けていく数列です。 数列 a_ {1} a_ {2} a_ {3} a_ {4} a_ {n} が等比数列だとします。 この等比数列の公比を r だとすると、 a_ {1}=a_ {1} ←初項 a_ {2}=a_ {1} \times r a_ {3}=a_ {1} \times r^ {2} a_ {4}=a_ {1} \times r^ {3} このように初項に公差を加えていくので、次の数列の一般項を求めよ。 1,3,9,27, ‥‥ 考え方 前の項に3をかけると次の項になるので等比数列である。 解答 a（初項）＝1， r（公比）＝3を代入して a n ＝1・3 n1 ＝3 n1

48s96ub7b0z5f Net Touhisuuretsu

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

8/2/19 公比が正である等比数列の第4項が12，第6項が192であるとき，この等比数列の一般項を求めよ。 一般項 \( \displaystyle \color{red}{ a_n = a r^{n1} } \) の式を使って，\( a \)，\( r \) の連立方程式を作り，それを解いて一般項を求めます。

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

An Bn An3n 1bn2n Bn Descubre Como Resolverlo En Qanda

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

Excel エクセルで等比数列の和を計算する方法

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

48s96ub7b0z5f Net Tousa Suuretsu

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座

漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

等比数列について 写真の問題の解説でrは実数であるからr 2とあります Yahoo 知恵袋

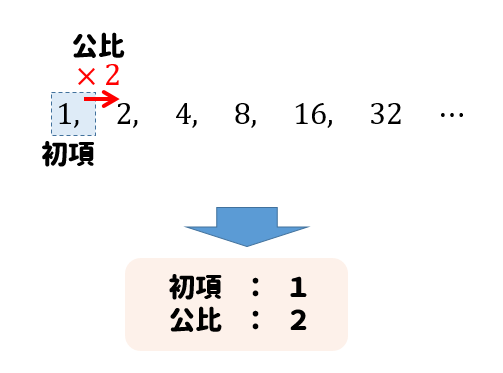
等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

例題で学ぶ高校数学 等差数列 等比数列 型の数列

無限等比数列の極限 おいしい数学

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

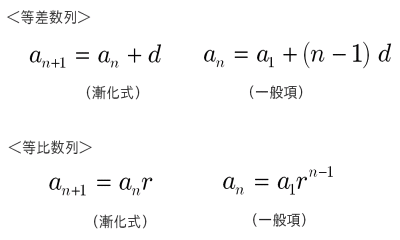
数列 漸化式と一般項 大人が学び直す数学

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列と等比数列の積の和の問題の解法ポイント 数列

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列の問題です 第4項が24 第6項が96である等比数列 An の一般 計算機科学 教えて Goo

等比数列の一般項について この回答の仕方では不正解なんですか 等 数学 教えて Goo

高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月

等比数列 一般項や和の計算 数学の偏差値を上げて合格を目指す

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

等比数列の和から一般項の求め方 １ 高校数学ｂ Youtube

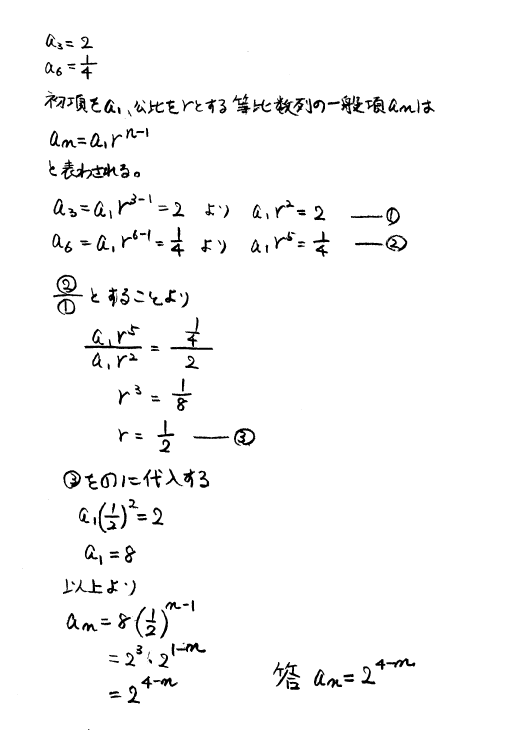
等比数列 一般項

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 7 8

誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう

漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

等差 等比 の和 2次式 等比 の和 おいしい数学

48s96ub7b0z5f Net Tousakakerutouhi

等比数列とその一般項 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

高校数学b 等比数列 A N の一般項 １ 映像授業のtry It トライイット

等比数列の一般項と和 おいしい数学

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

1

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

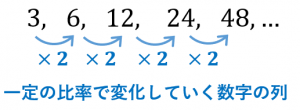
等比数列について 意味 一般項 和の公式まで詳しく解説 具体例で学ぶ数学

等比数列の一般項と和 おいしい数学

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

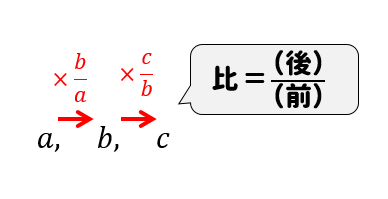
等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

等比数列の一般項 高校数学ｂ Youtube

1

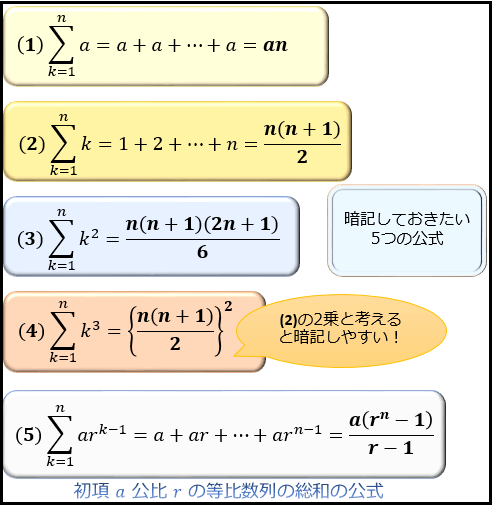
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

3

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

特性方程式とは より難しい漸化式の解き方 特殊解型 アタリマエ

等差数列 等比数列の一般項 和の公式 求め方を確認 Youtube

等比数列の和の公式は何故2個あるのでしょうか 赤で囲った2個 Yahoo 知恵袋

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

高校数学b 等差数列と等比数列の共通項の数列の一般項 受験の月

An 1 Pan Q型の数列の一般項の求め方 等比数列型に帰着させる

等比数列の一般項の問題です 解説をよろしくお願いします Clear

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の初項と公比の求め方が分かりません 教えて下さい １ Yahoo 知恵袋

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

等比数列の一般項と和 おいしい数学

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

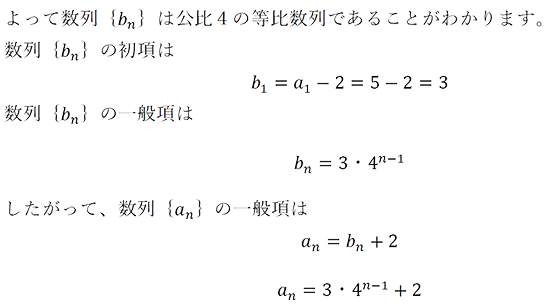
漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

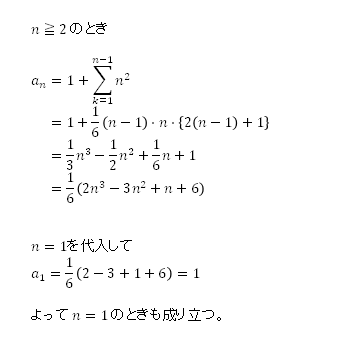
数学専門個別指導塾 Motoゼミナール 数列の一般項の賢い求め方 問題付き

無限等比級数の収束条件は 初項 と 公比 に注目

等比数列の和の計算で なぜn乗ではなくn 1乗なのか教えて欲しいです Clear

等差数列 等比数列の一般項とその和の求め方 Webstation Plus

等比数列の一般項は 1分でわかる求め方 和の計算 等差数列との違い

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等比数列の一般項と和 おいしい数学

無限級数 無限等比級数とは 和の公式や求め方 図形問題 受験辞典

高校数学b S と等差 等比数列の和 映像授業のtry It トライイット

階差数列

1

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

無限等比級数とは 導入と公式を解説 高校数学の知識庫

等比数列の公式まとめ 一般項と和の公式を分かりやすく解説

D 2 93 Aibm M Descubre Como Resolverlo En Qanda

数列と級数 Of 京極一樹の数学塾会員頁

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

数列と級数 Of 京極一樹の数学塾会員頁

Incoming Term: 等比数列 一般項 求め方,